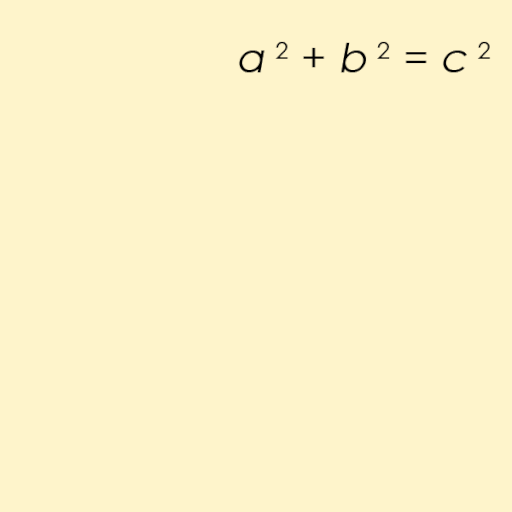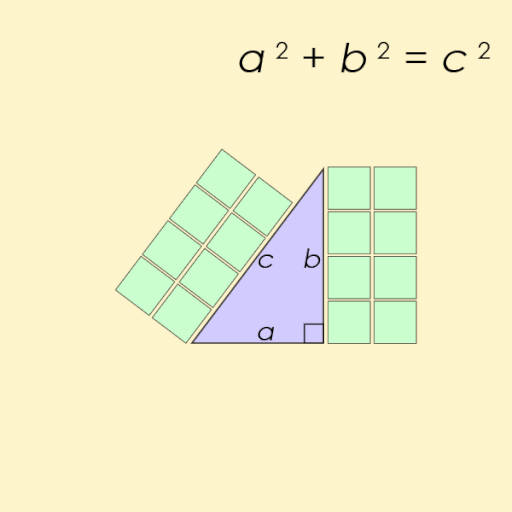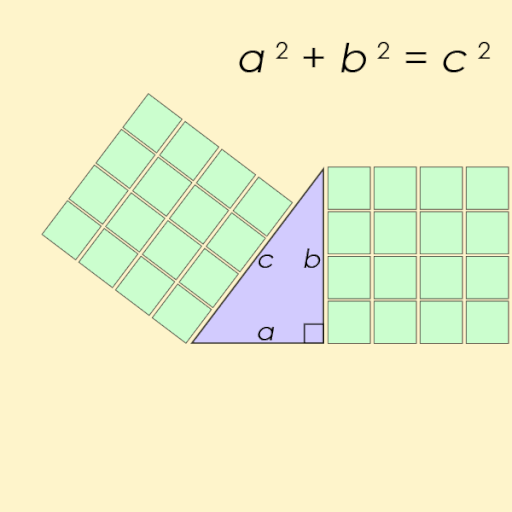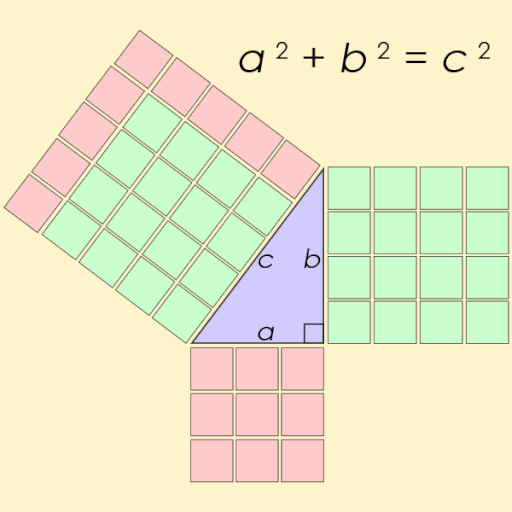Pythagorejská trojice – Wikipedie
Pythagorejská trojice je v matematice trojice přirozených čísel ( a , b , c ) (tj. celých kladných čísel), které lze využít jako velikosti stran pravoúhlého trojúhelníka.
Pythagorejská čísla a pythagorejské trojice – Matematika.cz
Pythagorejská čísla jsou trojice přirozených čísel, pro která platí Pythagorova věta – tedy, že součet čtverců dvou menších čísel se rovná čtverci třetího čísla z dané trojice.
01_Pythagorejske trojice_2022 | školský portál jihomoravského…
Materiál Pythagorejské trojice je určen zejména čtenářům s hlubším zájmem o matematiku. Obsahuje rozšiřující učivo vycházející z tématu Pythagorova věta, Pythagorovu větu zasahuje do historického kontextu, vysvětluje, jak s Pythagorovou…
Pythagoras – Wikipedie
Pythagorejská tradice měla velký vliv na Platóna, byla živá v novoplatónismu, v renesanci a v různých – často fantastických – podobách žije i dnes.
Matykání XXII: Jak si nabrnkat pythagorejské trojice | Matfyz…
Trojice přirozených čísel se nazývá pythagorejská, pokud reprezentuje tři strany pravoúhlého trojúhelníka. Nejznámější takovou trojicí je (3, 4, 5). Dnes se podíváme, jak lze vygenerovat ty ostatní pomocí čtverců komplexních čísel.
Pythagorejské trojice :: MEF
Nejznámější takovou trojicí je trojice (3; 4; 5), kterou využívali již staří Egypťané k vytyčování pravých úhlů. Je-li navíc (x; y; z) pythagorejská trojice, je pythagorejskou trojicí i trojice čísel (kx; ky; kz), kde k je přirozené číslo.
Pythagorejská čísla | Eduportál Techmania
[1] Seibert, J. Pythagorejské trojice trojúhelníkových čísel. Matematika Fyzika Informatika: časopis pro výuku na základních a středních školách, 2004/2005, roč.14, s. 385-393.
Pythagorás – život a esoterní nauka
29. 9. 2022Zázračný muž boží a zakladatel velice vlivné a zvláštní školy. Víme o něm skoro jen z mnohem pozdějších legend. Školu tvořili esoterici a exoterici, alias matematici a posluchači. Překvapením je, že tou vědeckou částí byli esoterici!
Struktura zobecněných Pythagorejských trojic | Digitální…
Zovšeobecnené pytagorejské trojice|diofantické rivnice|číselné teleso|okruh celistvých prvkov číselného telesa|ideálová triedna grupa
Scienceworld | Úloha: Pythagorejské trojice
Otázka zní: dokážete ke každému celému číslu většímu než 2 najít takovou dvojici, při které bude zadané číslo jednou z kratších stran (odvěsen) pravoúhlého
Pythagorejská trojice
Pythagorejská trojice je v matematice trojice přirozených čísel ( a , b , c ) (tj. celých kladných čísel), které lze využít jako velikosti stran pravoúhlého trojúhelníka. Tyto celočíselné kombinace byly využívány již ve starověku a jsou dones využívány v běžném životě (např. vyměření pravého úhlu na stavbě pomocí provázku s uzly ve stejných vzdálenostech, případně vyměření pravého úhlu svinovacím metrem v násobku jedné z Pythagorejských trojic). Název pythagorejská trojice je odvozen od… Wikipedie
odkazuje na služby nejen od Seznam.cz.
© 1996–2025 Seznam.cz, a.s.
